essential questions – One of Thirty Voices

Oh yeah! I used to dream about my lessons… over and over during the night. I’d wake exhausted. Here’s an example of what I do now…

When you realize the students can’t ‘see’ the thing you are teaching them…

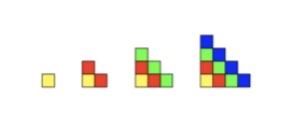
My kiddos are learning to write quadratic equations. This requires them seeing patterns of growth. The first lesson in this series was to help them see the growth in a pattern of cubes. I used a YouCubed lesson that involved coloring each growth step. Just that. This exposed several issues. The lesson with numbers was the next day, and I was pleased by the intensity of their interest, but here’s why I think that happened: I had prepared them for what they were looking for.

Color each growth step. Image from Stairs to Squares Gr3-5, YouCubed.org

Quotes taken from the original FB post…

Beth Hanna McManus writes “My 8th graders… totally missed the concept that the altitude to the base of the triangle goes through the vertex and hits the base at a 90 degree angle. I explained this in mathematical terms, in layman’s terms, using words like straight to the base, “shortest distance”, had them draw them on the white boards (checking and helping each drawing) multiple times, had them label triangles. When it came time for homework, no one knew what to do. I flipped out and spent the rest of the day in a dither wondering what is wrong with me that I can’t communicate with these kids…”

When I plan a learning experience, I look for the base skill/image/idea a child needs to be able to have to participate in a lesson. It may be a simple warmup – for the triangle problem above, after realizing they didn’t get it, I might have them draw the altitude, pointing out the way the angle looks, and how it starts in the vertex, in several different triangles. Just that. No math, just letting them learn to see what they are looking for.

Starla Adams writes, “Yes, yes, and yes….says the teacher who is out of strategies to teach long division after Friday. I actually thought I was going a little bit insane for an entire hour.”

Teaching long division is challenging. I’ve worked with 9th graders who do not understand what dividing does. If they don’t have an understanding of partitioning and regrouping, long division is just a nonsensical set of steps that they must follow – and memorize. A warmup using manipulatives (coins buttons beads) to set the stage for dividing into groups would help them understand what they are looking for. Then long division can be taught as a routine to get there.

Another common student skill gap with division is poor factoring skills. A warmup (or preview lesson the day before) with a factoring math problem string like this video from Pam Harris, might help strengthen their math fact fluency.

While working on any new skill that requires factoring, try giving students a factor chart. They won’t be using all their working memory on remembering number facts, but on learning the process of the task at hand.

Learning plans should empower students…

I realized that my 9th graders didn’t yet know that they had the power to create their own understanding. They were waiting for me to tell them what to do. Danielle Love and Kay Butler point out ways to shift the heavy lifting (and learning!) to the students!

As teachers, we spend lots of time creating learning plans. Many of us already know what misconceptions kids have, and what errors are going to get made. So lets plan ahead to expose -and remediate and preview- so that these issues don’t cause student failure during the learning of new material. These little discovery sessions and warmups are critical to building understanding and are often worth every minute of time we spend on them!

By all means, overthink and go crazy, in a most productive way! Math teachers, you rock!! I would love to hear how other teachers prepare for these misconceptions and gaps!

(And no, I don’t have those recurring math dreams nearly as often anymore!😂)

Thanks to Shana McKay of Scaffolded Math and Science, and and this really interesting thread on her fantastic FB Visual Math!

“It is not as important that managers have succeeded with the problem as it is for them to have wrestled with it and developed the skills and intuition for how to meet the challenge successfully the next time around” The Innovator’s Solution: Creating and Sustaining Successful Growth Clayton M. Christensen, Michael E. Raynor The above quote applies to hiring good people to help businesses grow and succeed. I could change the word ‘manager’ to ‘student’ and define exactly what the career ready student must look like! Good companies know they will never find a perfect experience match, but instead will look for skills that allow the transfer of abilities. In math having the students actually work at solving math challenges will give them those transferable skills – and the confidence to use them! What does this process look like during an actual lesson? The initial introduction to this problem-solving task ‘stuff’ might present a challenge for both you and your classroom. It did for mine. I was following the pattern of ‘tell students the goal of the lesson’ (i.e. factor polynomials); run through the lesson with questions and discovery (felt like pulling teeth!), work problems with them; give them practice. My frustration was in the students’ comprehension- I could tell with my questioning that they didn’t ‘get it.’ ” Why don’t you just tell us?” one student even said. There was no desire to look for possible solutions. they just wanted me to give them the answers and accused me of not teaching them. The frustration on all sides stopped the learning process. I was asking them to do something they didn’t have the tools to do. I failed to train them in the method I wanted them to use! I’m here to keep you from making the same mistakes I did. Lay the groundwork first with mathematical thinking. Then get out of the way and be less helpful! Be Less Helpful I first heard this phrase while watching a TED talk by Dan Meyer. The genius of his approach, letting students look at a situation and decide how to solve it, was breathtakingly simple. It pinged deeply against what I was beginning to learn about in the common core ‘key task’ ideas. It fit in with my own ‘questioning and discovery’ method. I had to know more. What I found was a community (blogs and on Twitter!) of teachers who are committed to teaching their students through challenging tasks, and giving the students lessons as the child decides they need the skill to solve the assignment!” The difference? Nobody asks, “When am I ever going to use this?” They are putting their hands out for the teaching. They are engaged and interested because they are in charge of the process. The key to success is in choosing tasks that are going to teach the standards you want them to learn. Here is a good checklist for the tasks you want to use: 1. Identify the mathematical goals for the task: what standards will the students experience as they solve this task? 2. Identify how prior knowledge will be scaffolded. 3. Identify how students will demonstrate that the mathematical goals have been met. 4. Work the task in order to anticipate possible solution paths; ensure a variety of representations and/or strategies. 5. Identify common misconceptions. In other words- everything you always do for a lesson! Here is the difference: you are not going to tell them how to solve the task, or what methods or formulas to use. you are not going to remind them of where they have already seen the material or tell them how to start thinking about the task. You may or may not provide an illustration- the following task requires they visualize the triangle themselves. This is not the time for remediation lessons for kids missing skills. Let them struggle. As much as you want to give in and tell them what to do, don’t. Ramp up the questions to help the student find the entry point that fits their skill level. No, they may not get as far as the rest of the class today, but they will be further along than when they started! The task allows students to explore, investigate, and make sense of mathematical ideas on their own. Let it provide personal challenge and productive disequilibrium, too. Be less helpful! Here is an example of a key task: Teaching the Converse of the Pythagorean Theorem Students are told to envision a triangle, sides a,b,c, where side c is a specific given length. The task is to use various lengths for sides a, b and determine what effect the lengths have on angle C. (You may specify that sides a, b must be shorter than C, as an introductory exploration, but that is all.) As you go around the room, looking on as students individually engage the task, remember that you are not allowed to tell anyone where to begin. You should be ready to ask prompting questions (prepared beforehand) to give students ideas about entry points if they can’t get started. Have advancing ideas for students who get done quickly, (ask them to come up with a different method to do what they did, or ask them what happens when a,b are longer and shorter, or longer and longer). During the group work, listen for everyone sharing. Require that students justify and defend their work to the group. Be prepared with clarifying questions. If a student is changing their work because of another student, ask them to tell you what changed their mind- this articulation of ideas is critical. This is a good time to decide on selection and sequencing for the whole group discussion. Your goal here is to assess their learning and advance them toward the mathematical goals using questions (to prompt, to clarify, to restate). The whole group discussion is the opportunity for summarizing the learning from the groups. Encourage every student (I utilize Accountable Talk) to participate, either by sharing ideas, or restating comments from others. This is the place to make connections among solution paths- let the students make the connections (remember, we are being less helpful!) Don’t forget to tie in what they have done to the vocabulary. In the converse lesson, this is the place to tie the mathematics the students have used into one of the three versions of the converse theorem, (and to the standards goals for the lesson). It is important to have another problem or two that require similar (but not exact) engagement for ‘setting’ the skills they just used, and expanding on what they just did. Don’t forget this step. I believe in having students talk about what they have discovered- not to me, but to another student, or in a journal. This would be yet another step in formative assessment for learning. Or, I could have just asked the students to use the Pythagorean Formula, given the measurements for sides a,b,c and asked the whether angle C is 90 degrees. What do you think?