I’m Seeing Dots!

Do you number sense?

What I’m trying to ask is how comfortable are you with numbers? As children, we learn to count, 1, 2, 3… Then we begin to realize a one to one correspondence, that one isn’t just a number, it is a value, a penny or one fork, or one person. The bigger the number, the more items. We learn some rules for numbers: That one plus anything makes one more. That if we take away one, it makes the number smaller. Next thing you know we are adding and taking away all kinds of numbers. Then along comes place value and we learn to carry numbers; there are ones, tens, hundreds, thousands, ten thousands, whew! And for many children, each number becomes a solid thing, no longer fluent, no longer one plus one plus one makes three. Three is, well, three. It means a certain amount, and we no longer see it as individual items making up a whole.

I would like you to try an experiment.

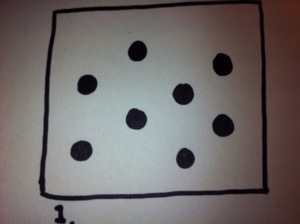
Without counting, take a look at image 1.

How many dots do you see?

Now quickly look at image 2. (Remember, no counting!)

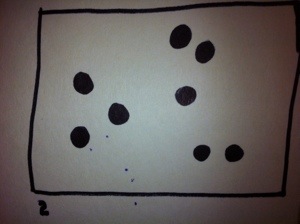
How many did you see this time?

Now think about how you saw the dots in each image. How did you group them or add them?
Which picture was easier for you? The neatly grouped dots or the randomly spaced ones?

Show the pictures to someone else. They will probably come up with the same number you did. Ask them to describe how they saw the dots, grouped them, made sense of them.

Was their method different? Did you like it better than your method? Will you see the dots differently the next time you look?

Whether you realize it or not, you have just made some new connections about the number eight.

Now solve for x:

4x = 3 + 3 + x

Did your new sense of the number 8 make the problem less complicated? Or did you pull out some algebra skills?

We rarely see dot cards used outside of first, second, or third grade here in the US. I think we may be losing valuable math fluency by not continuing to expose our children to these practices on a regular basis throughout their education. It is especially relevant now, as teachers are asking students to think about the different elements of math problems, asking them to make connections from one set of circumstances to another, expecting them to be able to break apart and re-form numbers like a set of Lego blocks. Yet, from my own observations, we have 7-12 grade students who lack a basic ability to do this.

We give them formulas that have no meaning, theorems for which they do not understand the proofs, and polynomials they struggle to factor or multiply, because they lack the ability to construct and deconstruct numbers. Algebra is difficult because they cannot see that x can be any number. In that exercise above, could there not be more than one right answer? Shouldn’t our kids be curious about that, check for that? (Bravo if you did!!)

Cathy Humphries uses dot card exercises with her 10-12 graders. She has this to say:

“Dot Card Number Talk Commentary:
Cards with configurations of objects, that we often call “dot” card number talks, establish important new principles for mathematics classes. While it may seem that these arrangements of shapes are only for young children, we have found that they are critical for older children – even high school students – because they help to lay the groundwork for changing how students think about mathematics. Dot cards do not suggest procedures that students are “supposed” to follow; instead, they encourage students to think about what they “see” rather than what they are supposed to “do.” This frees up students for learning new ways of interacting in math class.
Some of the things they can learn from dot card number talks:
• Just as people “see” things differently, there are often many ways to approach any mathematical problem.
• Explaining one’s thinking clearly is important. This requires that students to retrace the steps of their answers and learn to use academic language, where possible, to describe what they did to solve the problem.
• It is important for students not only to explain what they did, but why their process makes sense. In the case of dot card number talks, this involves where they “saw” the numbers they used. In the case of arithmetic operations, it involves understanding the mathematics that underlies any procedure that they use.
• The teacher’s job is to ask questions that clarify what the students see rather than how they “should” see.”
Cathy Humphreys.
Boaler, J., & Humphreys, C. (2005). Connecting mathematical ideas: middle school video cases to support teaching and learning. Portsmouth, NH: Heinemann.

Introduce a new fluidity into your classroom. Check out more about dot cards in this piece by Math Coach’s Corner.

If you have good number sense activities resources, I’d be happy to link to them here!

Is ‘Numerosity’ Humans’ Sixth Sense? (livescience.com)

Do You Speak Words of Life or Death?

“Thoughts become words, and words have the power of life and death. Think to speak life giving words to yourself and others.” Joseph Prince

These words put me in mind of how we as teachers have the power to create hope or plant failure in the minds of our students. Our students believe us. For good or ill, we hold all the answers (even when we don’t).

We can use that belief to inspire our students, to enable them to reach beyond anything they might be willing to do on their own. Here is one way:

Fixed vs Growth Mindset

Do your students have a Fixed Mindset or a Growth Mindset? Do they eagerly tackle problems, curiously start investigating the challenge placed before them, generate ideas for possible solutions?
If you give students a choice of assignments, do they pick the easy ones or the hard ones?
Do your best students want class discussion, or do they just want you to show them how to work the problem, so they can do their work and keep their A?

It breaks my heart when a student walks into class and says ‘I’m not good at math. Don’t expect much from me.’
Or the kid who told me, ‘whenever I’ve done enough to pass, I’ve been told that I usually quit trying.’ Or the A student who is afraid to try the problem until you have shown them how they are supposed to think about it. These students are exhibiting Fixed Mindsets. They have been given the idea, by teachers or parents or grouping or grades that they are dumb or smart or not good at math, or science, or too smart to fail at math, or science, or any other subject. Girls, especially, tend to get the message: math is not your ‘thing’; children are grouped by what teachers believe they can do: advanced, remedial or in-between – all a form of ‘silent’ stereotyping, as deadly as anything we say out loud. What message am I sending when I too quickly provide an answer, instead of asking good thought-provoking questions? How can I encourage a growth mindset?

What is a growth mindset, and how does it benefit our kids?

A growth mindset is the ability to see possibilities. It is a confidence in one’s ability. It is the MacGyver in all of us, to use a modern example. And it can be taught!!!

Teachers can encourage a growth mindset by changing the messages they give to their students:

“I believe in you”

Don’t let grades define your student. Instead of a grade, give specific feedback on problem areas. Tell them – put it in writing – that you are giving them the feedback because you believe in their ability to fix their mistakes.

Celebrate mistakes!

Your students are scared to death of making a mistake, getting it wrong, so they sit on their hands in class. Am I right? How frustrating is it to ask a question about the material and be greeted with blank stares?

It is time to celebrate (maybe even reward) mistakes. Sounds crazy, I know, but hear me out…

Tell the kids that every time they make a mistake and struggle with fixing it, their brain gets smarter. (Don’t worry, it’s true, check out this link: Brainology)

Reinforce the message:
Give them a picture of their head in profile with a brain drawn in it. Make sure the brain has lots of little empty spaces in it, like the one I’ve posted below (or break out the projector and let the kids make their own personal profiles on blank paper).

Tell them that each time they find a mistake, they get to color in a section of their brain. Celebrate the fact that their brain has grown! (Younger students like stickers; older students may want stickers, too! It doesn’t have to be anything huge.) I would even keep a big poster of a brain on the wall- on a really tough day, where the kids have made it through with lots of effort, color in a space on the class brain- they have become collectively smarter! This is also a great community builder. It’s like those scaling a wall, walking on ropes exercises where you can’t make it without everybody pulling together – without the parental permission forms!

And for those of you who aren’t sure whether you have a fixed mindset or a growth mindset, here’s a link to a great article, with a short mindset assessment at the end. Growth Mindset

And don’t worry if it tells you that you have a Fixed Mindset- it is only temporary!!

What did my results say? What do you think? Am I a Fixed or Growth mindset kind of person? I can’t wait to hear what you think!

A Lesson Starter: Unraveling the Vocabulary

“You’ll know kids mastered a subject if they have the vocabulary to talk about it intelligently.”

This comment was part of a recent post “It’s Building Kids’ Vocabulary, Stupid” published by Educationnews.org.

Vocabulary is critical, especially in math. Look at the language used in the Common Core standards – you have to be a mathematician to understand what each one means. To clarify the purposely brief standards, teachers in Tennessee are being provided with EU’s, essential understandings. EU’s are great, but when I tried to translate one recently, in order to write it in a way a student could understand as the goal for the day’s lesson, the vocabulary was still too dense.

A Lesson Starter: Unraveling the Vocabulary

Let’s say you have told your students that the goal for the day is factoring polynomials. You have given your students a key task designed to give them conceptual understanding about the topic. You have asked them to think about the problem and decide what they think they will need to do to work toward a solution. Then you realize that they don’t recognize the words factor (don’t scoff- my 10th graders didn’t) and they have no clue what a polynomial is.

Instead of defining the words for them, or having them copy some useless definitions out of the back of the text, let them spend some time defining what they think the problem is asking them to do.

Next, have them share in small groups and agree on the actions/terminology the problem requires. Then bring it into a whole group discussion. Have the students agree as a group on the terminology they are going to use as they work their way through the assignment. Use clarifying and summarizing questions as necessary to allow the students to come up with a common vocabulary.

Don’t worry if the students don’t use the formal math vocabulary for the assignment. It’s okay not to. In fact, allowing them to use familiar vocabulary will boost their confidence for when they need to tackle other, less familiar projects.

Once the assignment comes to a close, draw the students back to the formal math vocabulary. Ask them to decide how what they just did matches up with the formal definition. Let them come up with valid connections and understandings.

Then have them explain it to another student. Listen during this process. Ask some students to share their understandings with the class. If there are different ways of explaining, (which there usually are!) have students indicate which way they understand best. It is not a contest, it is a chance to show children that there are lots if different ways to come to understandings.

Finally give the students another problem with instructions in the same formal vocabulary that they just defined. This will allow an even stronger connection to the newly learned term.

(I like word walls, so the new term would definitely be added at this point.)

Dear reader, I would love to know if you were able to use this idea in your classroom.

Join The Math Revolution!

Check out this exciting website!
Jo Boaler is giving teachers and their students the tools and information we will need to begin loving math.

We all want to see Key Task lessons, what they look like, how students react, what it means when students start conceptualizing math. There are videos, lesson ideas, and links to publications and research.

The site is called YouCubed,
“a nonprofit providing free and affordable K-12 mathematics resources and professional development for educators and parents.”

Be among the first in your block:

I invite you to Join The Revolution!

www.youcubed.org/

A Reply to Why Johnny Can’t Tell Us Why

The author writes: “Johnny (a.k.a. Mary, Bobby, Dashawn, Jaynaya, etc.) can’t think. He doesn’t have the basic mathematical understanding of how the operations work, the nature of numbers, and the fundamental “rules” of the game of math. She doesn’t have the “self talk” skills to decide what to do when she doesn’t know what to do. He doesn’t have the confidence to just read the problem, take it one step at a time, and TRY. She doesn’t have any tools in her problem solving toolkit aside from learned helplessness and the response, “I don’t know” when posed a question.” http://www.rimwe.com/the-solver-blog/41.html

The link I’ve posted is the author’s full blog post on this topic. From my own experience, I believe it describes what is happening in high school classrooms across our country. The author asks the question, “What strategies or techniques have you found that are helpful in trying to turn the tide? Well, I’ve spent my summer trying to find some of the answers this author is asking. Here is my response.

You were in my class last year, weren’t you?!! Same background, different ethnicity. These students required that I fed them everything and when I didn’t, they fired me as their teacher. I have spent my summer looking for answers to your questions. I believe I have found some powerful answers. I even started a blog to talk about some of these solutions:

Inquiry, task oriented learning;
Mathematical thinking;
Visualization;
Number sense practice as part of every class;
Encouraging growth through mistakes;
Small group discussion;
Questioning that encourages students explain what they are thinking.

Oh, wait, you wanted something to deal with the anger and the apathy. That is a much tougher question.
I think students have gotten the message that they are not good enough – at math, at English, at any class. I think the response is frustration, after all, wasn’t school supposed to give them these skills? They showed up for class, they did homework or reports or worksheets. Why is it now not good enough? I’d be angry, too.

We could spend years blaming, wishing, and wringing our hands, but let’s not.

You and me and the teachers (and the parents of these children who are frustrated and unhappy with school) who are faced with this scenario are going to have to work with what we’ve been given. As for me, I am going to meet the kids where they are, use number sense puzzles and practice (as simple as I need to go, first grade level if necessary) and begin teaching these kids a new way to think about math.

Will I have to re-earn their trust? YES! It won’t be easy, but for ANY of this talk to be of any more use to our children than anything else the education community has done, for our kids to make it through these new assessments (which we really need to rethink, but that’s for another post); for our kids to make it into colleges, to have good lives, to be good citizens, we are going to have to change the message we are sending our children. They are good enough! They are clever enough to learn ANYTHING! School can be enjoyable and rich and kids can like math and literature and science and history. Anyone who tells you not to expect it, is damaging what the experience is supposed to be. Will it be struggle and hard work? Yes. And that is perhaps where we have let them down the most.

We are afraid to let our children struggle.

Did you know that every time you have to solve a puzzle, work out a problem, or struggle to master a skill, your brain grows? Research shows that synapses fire every time this happens. Mistakes, failures, do-0vers are NOT BAD! These are things that have to happen for us to learn. For me, that means giving my math students rich, complex questions to think about, to examine, and discuss. And maybe solve.

The methods listed above are a start: Belief in our kids, funding schools, giving teachers the knowledge, as I have gained this summer, to teach kids through problem solving – not rote memory and regurgitation – and stopping the insanity of using test scores (we can look at student’s faces and observe their behavior – a focused, well-behaved student, eagerly digging into a lesson because they are interested!) to see if they’ve learned anything is what will ultimately make a difference for our children’s education.

I hope to address some of the topics I’ve touched on here in future posts. I welcome any comments, experiences, resource/research links, lesson ideas, etc. that will expand upon these conversations. Thanks for reading.

CCSS: Key Tasks and Scientific Method

Common Core State Standards (CCSS) are lists of things kids are expected to learn in each subject during each school year. They are not the actual lessons. Your child’s teacher and school system will decide what lessons to teach and how to teach them.

Research shows that one of the best ways to teach children is to give them tasks and have them work through the solutions to the tasks. The child is given directions as needed, or small lessons on specific skills, but the child is allowed to figure out what skills they need, or what they need to know, to accomplish or solve the task. These are called Key Tasks.

To be able to participate in the process of Key Tasks, a child needs to have a way to approach and organize the information. In mathematics, this process is going to feel very different than the existing process of “show the child the problem, work the problem with the child, and then let the child practice problems. Without setting up the structure of the process first, students may feel that the teacher has abandoned them, is not really teaching them anything, or worse. It takes time to transfer responsibility for problem solving when a child has never been asked to shoulder the responsibility (except for remembering how to do some practice problems, or work a formula – not really learning, just memorizing and regurgitating information).

The process of approaching and organizing the information is very similar to the scientific method. Any teacher or parent can help a child learn how to approach these new key tasks by teaching them a “mathematical thinking” process. The steps in the process are simple ones: Read and think about the problem, draw the problem or restate the problem, discuss the ideas about the problem with others or use resources (group discussion), estimate the answer, “mathematize” the problem (a formula or equation), try/refine/rethink, see if the answer makes sense. These steps may need to be used more than once throughout the process. As you can see, the actual answer is only a tiny part of the process.

For teachers, here is a brief lesson for teaching students how to use mathematical thinking in the class. For parents, you can help your child use this pattern with their math homework:

I love the idea of math as a thinking process. Instead of just giving students the list of actions, , I would approach this the same way I like to approach setting up classroom norms. I would start with a sample problem and just have the students think about it. I would tell them not to try and solve it yet. Then I would have them verbalize their thoughts in small group and then whole group- we would write the thoughts/assumptions on a big sheet of paper titled ‘Thinking’ and tape it to the board. I would facilitate with clarifying and summarizing questions.

The next step would involve visualizing. Students would be asked to draw a picture to illustrate what they saw happening in the problem. Again in small groups, they would create a picture/illustration, titling the poster ‘visualize’. The posters would go up around the room. At this point, I would ask all students to move around the room ( in groups) and visit the posters to see if the illustrations made sense, and if they suggested any mathematical way to look at the problem.

Returning to their seats, each group would create another poster titled ‘mathematics’ showing the calculations / solutions that they came up with. Those would go up on the wall. Each student would then be instructed to visit each mathematics poster and decide if those mathematics/answers made sense in light of the problems. This might be a good place for the students to use sticky notes and place comments or questions onto the posters.

The groups would then go back to their posters, check out the comments (as would I, so that I could come up with more questions) and we would come back to a whole class discussion to examine the various mathematics and reasonableness of answers. I might put up an empty poster titled ‘revisions’ so that students could add ways that they will need to revise their own thinking to solve this and future problems.

The summing up of the lesson will not be right or wrong answers, but a summary of the process itself. The students will be asked to discuss with one other person what steps they went through to solve the problem, and then write a brief paragraph in their math journal about what steps they took to solve the problem.

The final poster, and the one that will remain on the wall for future work, will be the steps the students noticed were common to the process- maybe have each group list a step (different colors, handwriting?). This will give them a roadmap to solving future problems- and as the teacher, I will give them the time to use the steps as we move through the learning process.

Parents can help by giving your children the time to verbalize problems to you or draw what they think the problem represents. You don’t always have to know how to do the math to help your child think through the process. Even if they don’t come up with a “right” answer, or maybe all they have come up with is questions, the thought process is going to give them a way to get in on the next conversation in class.

Subtraction or Adding a Negative: Tracking change

In response to a recent article about the state of teaching of subtraction in schools vs teaching children to add the inverse or the negative: Mathematical computation is about change, movement. (Link at the bottom of the post.)
To move along the number line, in whatever direction, or plot one point to another on the Cartesian or imaginary planes, is to chart change. The direction, positive or negative depends on the starting place.
The example: Jonathan has two apples, but if you subtract one, how many does he have, is not about a negative apple (there us no such thing!) but about the change with respect to possessions; the movement from one amount to another. It is relational, depending on who holds the apples and who is receiving the apple.
Astronomy led to expression because of the movement of the heavenly bodies. Calculus is the expression of movement of all sorts of actions. The “rules” of math; why 2 acts the way it does, set definition, the differences of movement in a Euclidean world vs a spherical one- all of the rules are predicated on understanding and defining observed change, or predicting future change.
Somewhere along the way, the vision of math, the way we share this lovely process with our children, has been turned into some cookie cutter process. We lose the observation of this movement by disconnecting it from change and giving children math problems with no relationships to anything but counting. Showing that numbers can be broken apart and recombined, that they are fluid and can show change, (number sense we call it) is critical to math knowledge.
Subtraction is movement away from the center of one person or place- addition is movement toward a person or place. It is relative to the location of center.
As we get older, more mature, we begin to understand that we are not the center of the universe. Until then (and this is the teacher in me) we believe we are the center, that movement away from us is loss- subtraction, if you will. Take-away is a valid way to teach movement away from (possessions like apples moving from one position to another, or reducing numbers by other numbers, or defining the distance from ground to sub-basement, or of one planet’s orbit around the sun), especially to younger students.
As students get older, we can continue with the idea of movement: the concept of adding a negative number works well on a number line. It serves to explain the process of movement – in the multiplication of negative and positive, or negative and negative, numbers. It is a difficult idea for students who do not grasp the true nature of numbers. The words used to describe what is happening in math and the ensuing confusion are understandable- perhaps as suggested by a colleague who creates mathematical texts, we can simplify the terminology. Until then, we need to teach and talk about mathematics in as many ways as we can. There are so many ways to get to the accurate answer, one of them is sure to resonate with our students, or with each other as mathematicians, and each can be the correct way, no matter the language.

Link:

http://www.jonathancrabtree.com/about/yes-virginia-subtraction-like-addition-does-exist