Two roads converged in a yellow wood, and I- I took the road less traveled by, and that has made all the difference.
From “The Road Less Traveled”, a poem by Robert Frost
Mastodon??? MATHStodon!!! Join Us!
(From Sam Shah and Julie Reulbach) What We’re Doing and Why: Okay, friends. Twitter was acquired by Elon Musk and seems to constantly be on the brink…
Mastodon??? MATHStodon!!! Join Us!
We are getting the band back together! (That’s how it feels, anyway.) join us at Mathstodon.xyz!
Changing School: from a place where the rules are known to a place where the rules are not so clear.
This started as the third blog post in a series of conversation starters on a different way to structure the high school experience, and why Academy high schools are uniquely positioned to make the change. Then COVID 19 happened.
In two previous writings here and here, I proposed that we introduce students to high school with an overall checklist of goals for learning that ditches the standards approach. I dubbed it The List. The second post generated a great conversation on Facebook on the Modern Learners page that I gathered into a google doc here. There were two strong questions/statements that I wish to explore in more depth: Who creates The List? and, How do we balance It with student agency, and flexibility? Today’s blog post topic deals with who might create The List, and why current conditions may mean that it’s creation has already begun.
Here’s what has changed.
On March 12, we were sent home, and told we would be teaching from home for the next week due to COVID 19. As we all know, that week turned into ‘the rest of the year’. The scramble to teach online was real. It was exhausting. It was difficult and less than stellar for many reasons. It was also a real eye-opening lesson.
What are the critical takeaways/connections our kids needed to make during online learning? How do we keep students engaged online? How can we assess learning?
My school district, along with many others, has had to decide on what learning is going to look like this Fall. Face to face (F2F), digital learning (DL), or a blend of both. They gave choice to parents of the above via surveys, assuming F2F for any parent that did not respond. They sent surveys to teachers to find out who was planning to come to work, and who had reservations and needed to talk to someone. These actions cover attendance and health concerns.
As a teacher, my concern is what my students are going to be learning. I am concerned about relationship building, social-emotional issues, and math topics, pretty much in that order. So, what does this have to do with The List?
As of today, July 16, 2020, While I would prefer a digital-only start to my school (in Georgia), we are going F2F. The start date for F2F, as of today, has been pushed back a week to August 12. About 60% of our student population has chosen (or been assigned through not choosing) F2F. The others will be online. Teachers are being tasked with teaching the standards for their individual subjects, while students navigate masks, social distancing, one way halls, lunches in classrooms, rigid expectations for safe social behavior, and constant cleaning and sanitizing. Let’s not forget the restless political climate, sensitivity to stereotyping, and regular discipline issues.
The List in the current climate would allow us to identify Key Standards (also called power standards, something many of our teachers have already started), and streamline our lessons to reduce teacher and student fatigue. This could also assist in reducing the amount of interaction during F2F. I think we have a unique opportunity to work with our students to help them identify their passions.
Who creates The List?
My thoughts center around Who: the team that would actually create the initial list; and What: that there would be flexibility built into the list – that it would be able to grow and change with the student. Student agency will be covered in the next post, and I will spend a little more time on this statement from the very first post:
That first project is really where you learn how to do everything. The first few weeks of high school, you learn about the academies and you are encouraged to pick your project. There are lessons on how to break down your project by tasks. I took a quiz to find out what I was interested in for my first project. Some kids come in knowing what they want to do. I wish I had gone to the summer workshop. I could have started my project so much sooner!”
The List is a possibly powerful way to engage our students, create realistic learning targets, and relieve some of the classroom exposure burden created by the F2F mandate.
The benefits of The List in the current environment of reduced student contact and beyond.
- Students have clear targeted outcomes that they work on individually.
- Students learn as they need the information to complete projects
- Retention of knowledge is increased because students own and use the learning.
- More time is available for teachers to observe and help students, and for grading of projects and giving feedback; less time is spent lecturing/pushing the information.
- Students working on specific pathways are in specific areas of the building, staying limited to particular areas, not intermingling with 6-8 other classrooms of approximately 30 students each (on average) or in hallways with hundreds of students. Like home rooms, only based on the pathway, students are assigned to particular areas or classrooms in the building.
- Even when in school, teachers can hold zoom meetings synchronously with students at specific class times, wherever the students are in the building for any subject
- Computer areas can be set up in cubicle form using simple clear plastic dividers; students don’t change areas at all during the day.
For The List to be effective, the student must be courageous enough to identify their passions, which may be different from their best friend’s. While the initial list is the school’s, the parts that will be motivating and meaningful are chosen by the student:
I was wondering about the list that students were given at the beginning of their high school career…who generates the list? I read that students have choice in the order and way list gets completed, I’m wondering if the kids have any say over what is on the list? Noreene Thibault-Chen from FB discussion.
Since I’ve begun this particular thread, something of interest happened in my school district. A new STEM school opened, and it bears the hallmarks of what I have been speculating….
In this case, The List is actually tied to the student pathway. There are core items on these paths, but they are more embedded in the path than separate, unconnected classes. Think of the items on the List more like stations of learning on the way to a goal.
The List would contain core items, but also have specific steps /learning needs built into the pathways. The List will be created by the goal. Not all schools have to offer all goals. As the STEM high school is not for everyone, so too could there be other specialties, such as the Fine Arts hub being developed at another school in our district.
Bottom line, pathways and The List for that pathway, take the emphasis off of taking multiple classes each day that don’t seem related to anything. The focus would on connecting student learning to their future on a daily basis, and create real motivation for students as they work on creating evidence of learning based on their passion/goals.
Evidence of Learning
An important aspect of learning is assessment. The conversation around testing and test security are issues for F2F and online. Requiring students to demonstrate learning through digital products is an excellent assessment tool, and fits nicely with our current need for distancing protections. It works in F2F situations as well as online learning. It can be tied to all learning targets. It can be used in small group learning (via zoom or google meets) in class or out of it. It can be formative or summative. Teachers (and others) can clearly see the level of participation digitally, can provide immediate and individual feedback or questions.
One Possible Source Document for ‘The List’
This is an example of the basic requirements, which could then be used to plan the personal journey of a student, based on the topics chosen as the student moves through the high school journey.
“It would not include courses or grades, but levels of proficiency in various areas. ” Inside Higher Ed
I encourage you to read the article, and check out the group’s website for yourself. I would rather focus on The List, what it might look like, and more importantly HOW it would be created, supported, and used.
Let us not mourn the ‘normal’ that we miss, but take the opportunity to look forward to the better that will come out of the change!
Do you think teaching math causes you to over think??? Almost like “going insane “…NaNa Dunn from a post on Visual Math’s FB page
Oh yeah! I used to dream about my lessons… over and over during the night. I’d wake exhausted. Here’s an example of what I do now…
When you realize the students can’t ‘see’ the thing you are teaching them…
My kiddos are learning to write quadratic equations. This requires them seeing patterns of growth. The first lesson in this series was to help them see the growth in a pattern of cubes. I used a YouCubed lesson that involved coloring each growth step. Just that. This exposed several issues. The lesson with numbers was the next day, and I was pleased by the intensity of their interest, but here’s why I think that happened: I had prepared them for what they were looking for.
Quotes taken from the original FB post…
Beth Hanna McManus writes “My 8th graders… totally missed the concept that the altitude to the base of the triangle goes through the vertex and hits the base at a 90 degree angle. I explained this in mathematical terms, in layman’s terms, using words like straight to the base, “shortest distance”, had them draw them on the white boards (checking and helping each drawing) multiple times, had them label triangles. When it came time for homework, no one knew what to do. I flipped out and spent the rest of the day in a dither wondering what is wrong with me that I can’t communicate with these kids…”
When I plan a learning experience, I look for the base skill/image/idea a child needs to be able to have to participate in a lesson. It may be a simple warmup – for the triangle problem above, after realizing they didn’t get it, I might have them draw the altitude, pointing out the way the angle looks, and how it starts in the vertex, in several different triangles. Just that. No math, just letting them learn to see what they are looking for.
Starla Adams writes, “Yes, yes, and yes….says the teacher who is out of strategies to teach long division after Friday. I actually thought I was going a little bit insane for an entire hour.”
Teaching long division is challenging. I’ve worked with 9th graders who do not understand what dividing does. If they don’t have an understanding of partitioning and regrouping, long division is just a nonsensical set of steps that they must follow – and memorize. A warmup using manipulatives (coins buttons beads) to set the stage for dividing into groups would help them understand what they are looking for. Then long division can be taught as a routine to get there.
Another common student skill gap with division is poor factoring skills. A warmup (or preview lesson the day before) with a factoring math problem string like this video from Pam Harris, might help strengthen their math fact fluency.
While working on any new skill that requires factoring, try giving students a factor chart. They won’t be using all their working memory on remembering number facts, but on learning the process of the task at hand.
Learning plans should empower students…
I realized that my 9th graders didn’t yet know that they had the power to create their own understanding. They were waiting for me to tell them what to do. Danielle Love and Kay Butler point out ways to shift the heavy lifting (and learning!) to the students!
As teachers, we spend lots of time creating learning plans. Many of us already know what misconceptions kids have, and what errors are going to get made. So lets plan ahead to expose -and remediate and preview- so that these issues don’t cause student failure during the learning of new material. These little discovery sessions and warmups are critical to building understanding and are often worth every minute of time we spend on them!
By all means, overthink and go crazy, in a most productive way! Math teachers, you rock!! I would love to hear how other teachers prepare for these misconceptions and gaps!
(And no, I don’t have those recurring math dreams nearly as often anymore!😂)
Thanks to Shana McKay of Scaffolded Math and Science, and and this really interesting thread on her fantastic FB Visual Math!
Making Math Formulas Tactile
The credit for this unusual idea goes to Math Giraffe and the Tactile Formula Project . Here’s how it played out in my 9th grade Algebra I classroom.
The challenge? Making Exponential Formulas out of concrete images
I believe the lesson is applicable with any formula and any level of student. Try it yourself… how well do you understand the formulas you teach?
The Lesson
I started by telling the students about ‘this cool idea I saw on the internet’.
The idea is to create formulas out of three dimensional objects, like candy or pennies, or legos, or cubes, or squares that suggest or seem to define the elements in a formula. I didn’t have the luxury of time to collect objects, so I told my students to use drawings of items that they planned to use to make the elements.
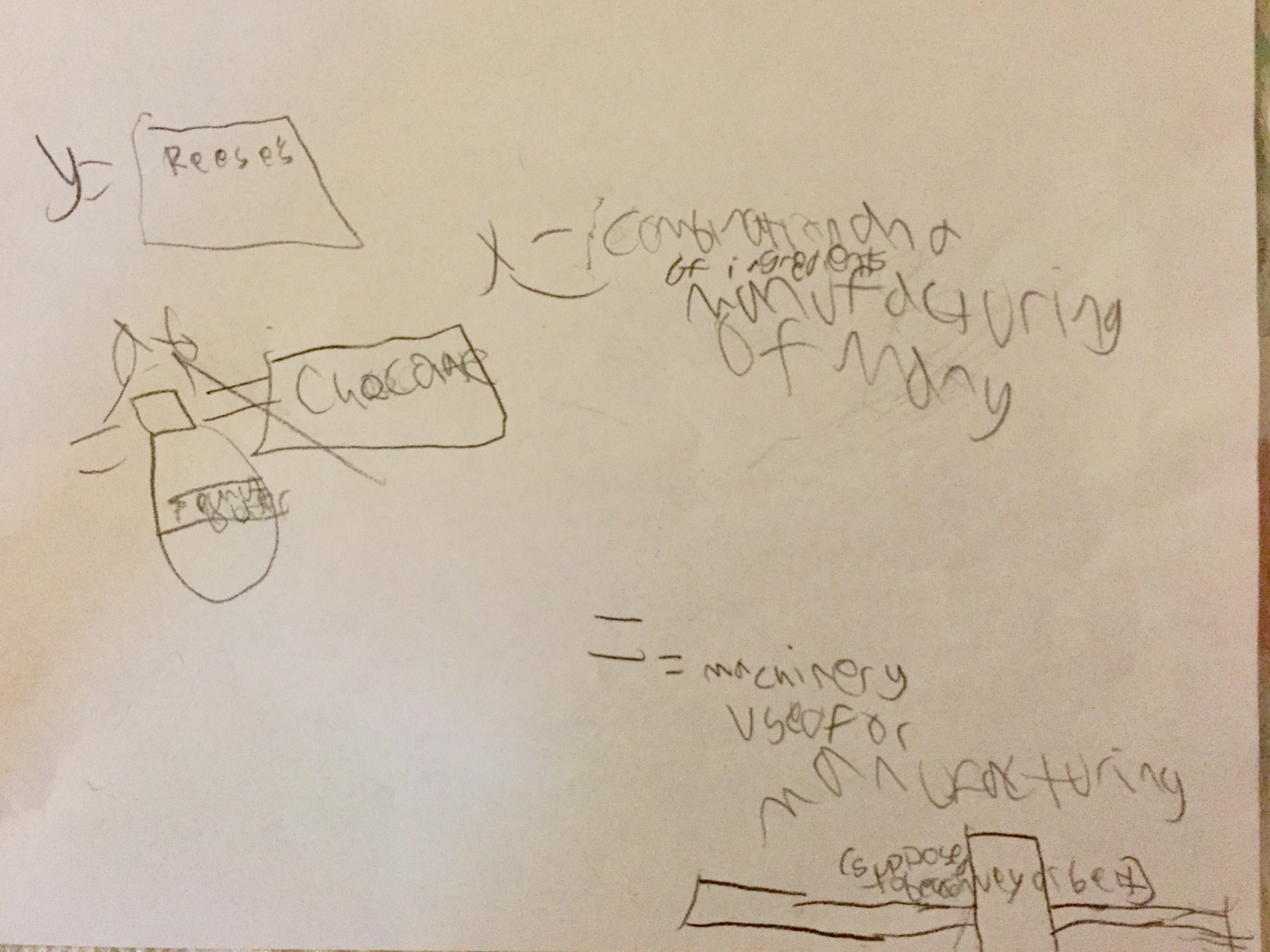
To get the creative juices flowing, I shared the images from the Math Giraffe blogpost, and started the conversation about what I saw in the images. The students quickly started noticing and interpreting what they saw in the images, and questioning why students used some of the images in the examples. Some students began interjecting their own ideas for images they would have used. This really primed the pump, so to speak, for the formulas we were going to interpret.
Images from Brigid’s Math Giraffe blog post.
Brigid, of Math Giraffe, used the classic slope-intercept formula,
y = mx + b
well known to my students. The task for my students was to do this with the multiple versions of the exponential formula:
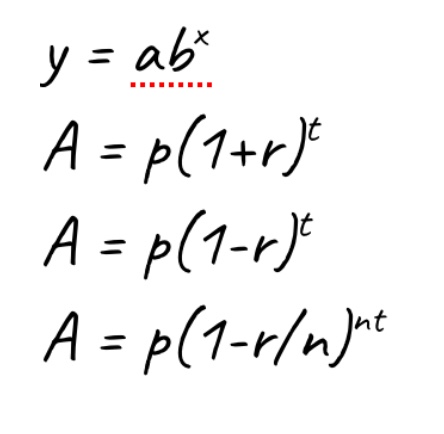
I wrote all of the different forms of exponential formulas on the board, and let each student choose the formula they wanted to use for their visual interpretation. What followed was a deeply enriching -and eye-opening – mathematical and conceptual conversation among all of my students!
Note: We used exponential formulas, but any formula would work with this activity.
The challenge for my students was using pictures to relay the action contained in the formula elements vs just using a picture that looked like an item in the formula. An example of this was incorrectly using bananas for parentheses, because, as the student explained, “they looked like parentheses.”
This student was just a little shaky on choosing an item that revealed the inclusive nature of the parentheses. Another student didn’t use any pictures at all. He wrote out his formula using a color for each letter, basically color-coding the identity of each element in the formula with an elaborate system for understanding each part:
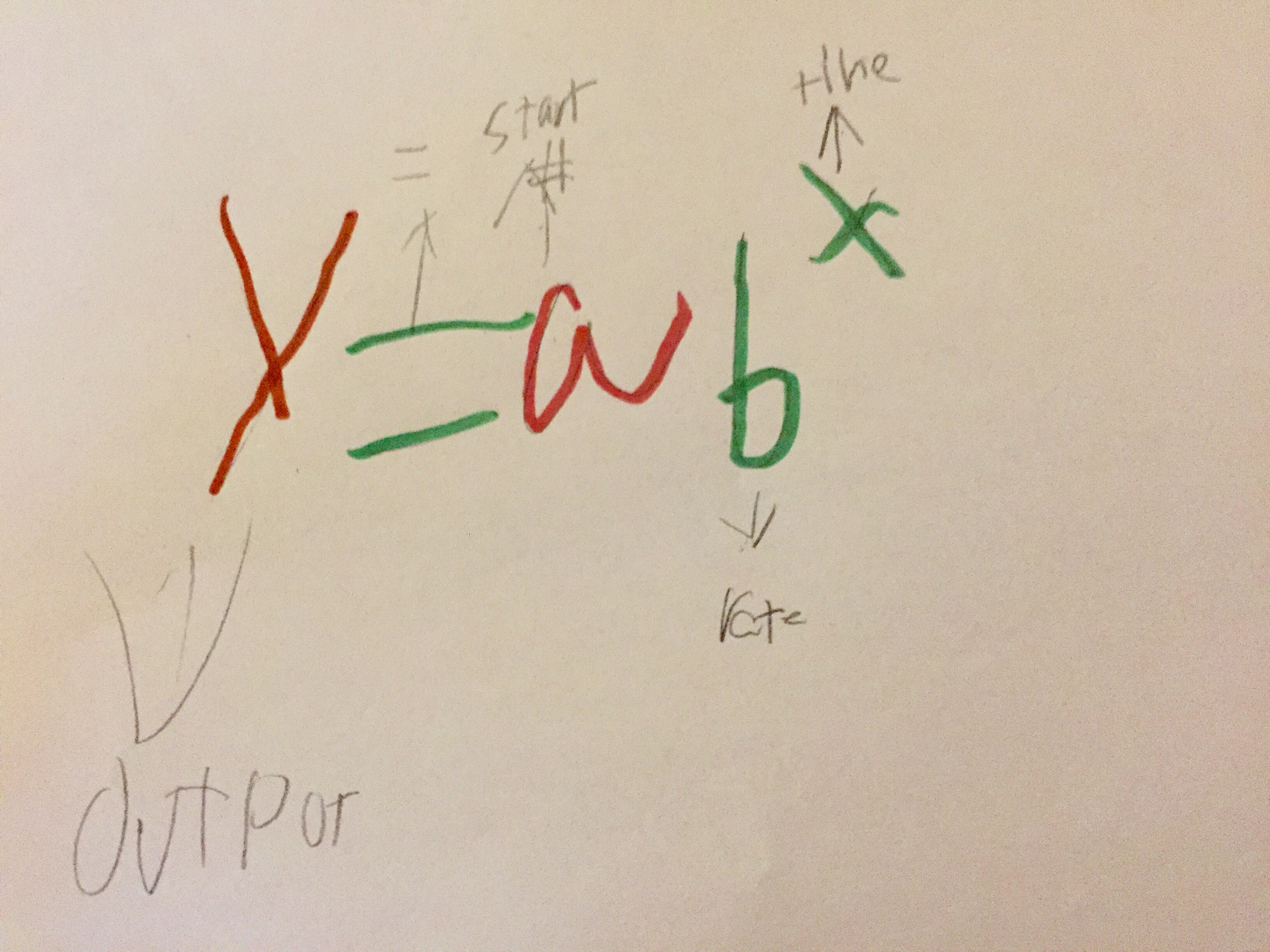
Did they miss the point? Absolutely not! Both were much more able to explain when and how to use the formula after this task.
This task got my students thinking more deeply about the formula itself, than just trying to memorize when to use it!
Interestingly, the exponential growth element was mostly identified as time, with one child drawing a clock face whose hands illustrated the exponent variable.
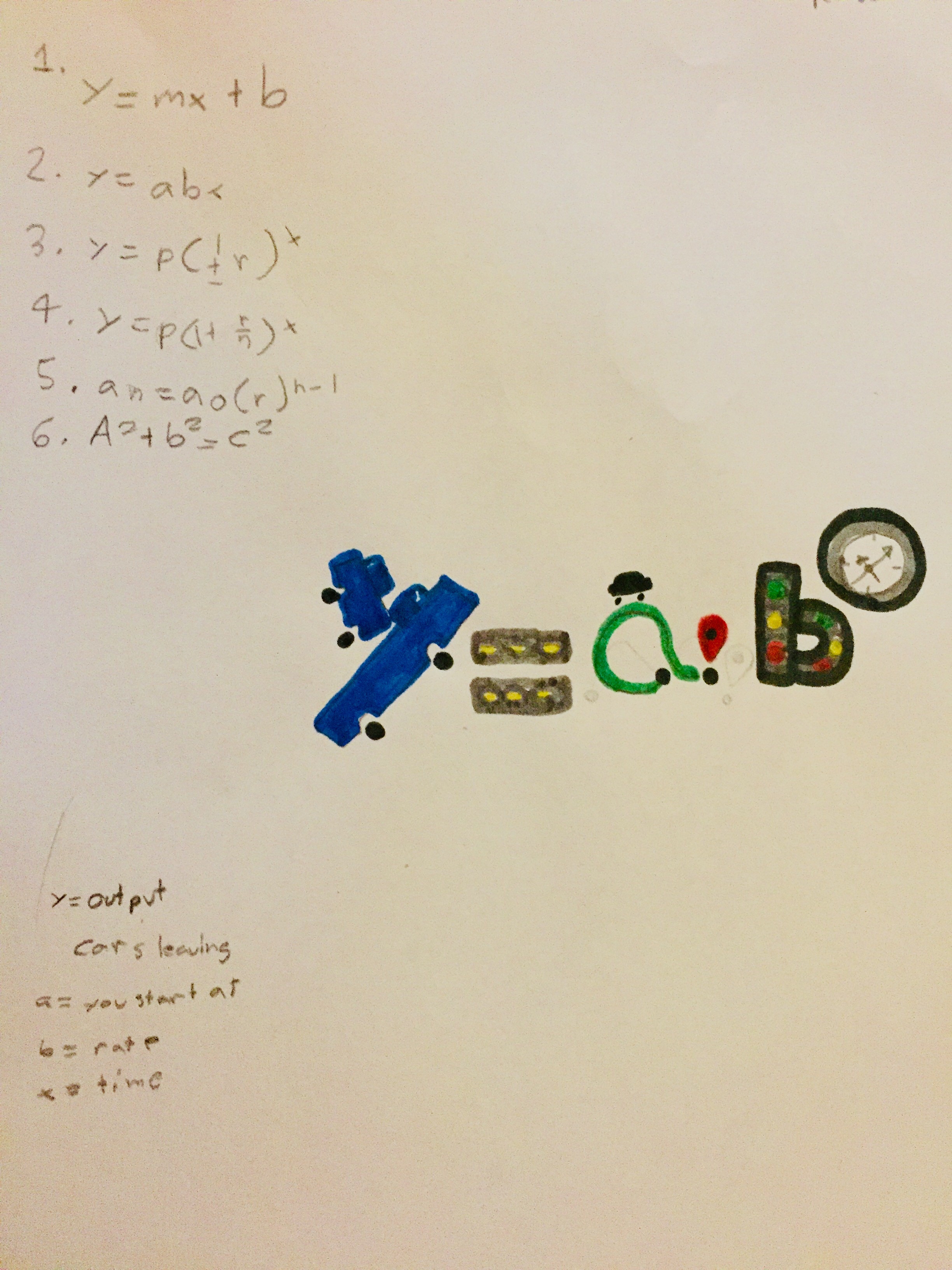
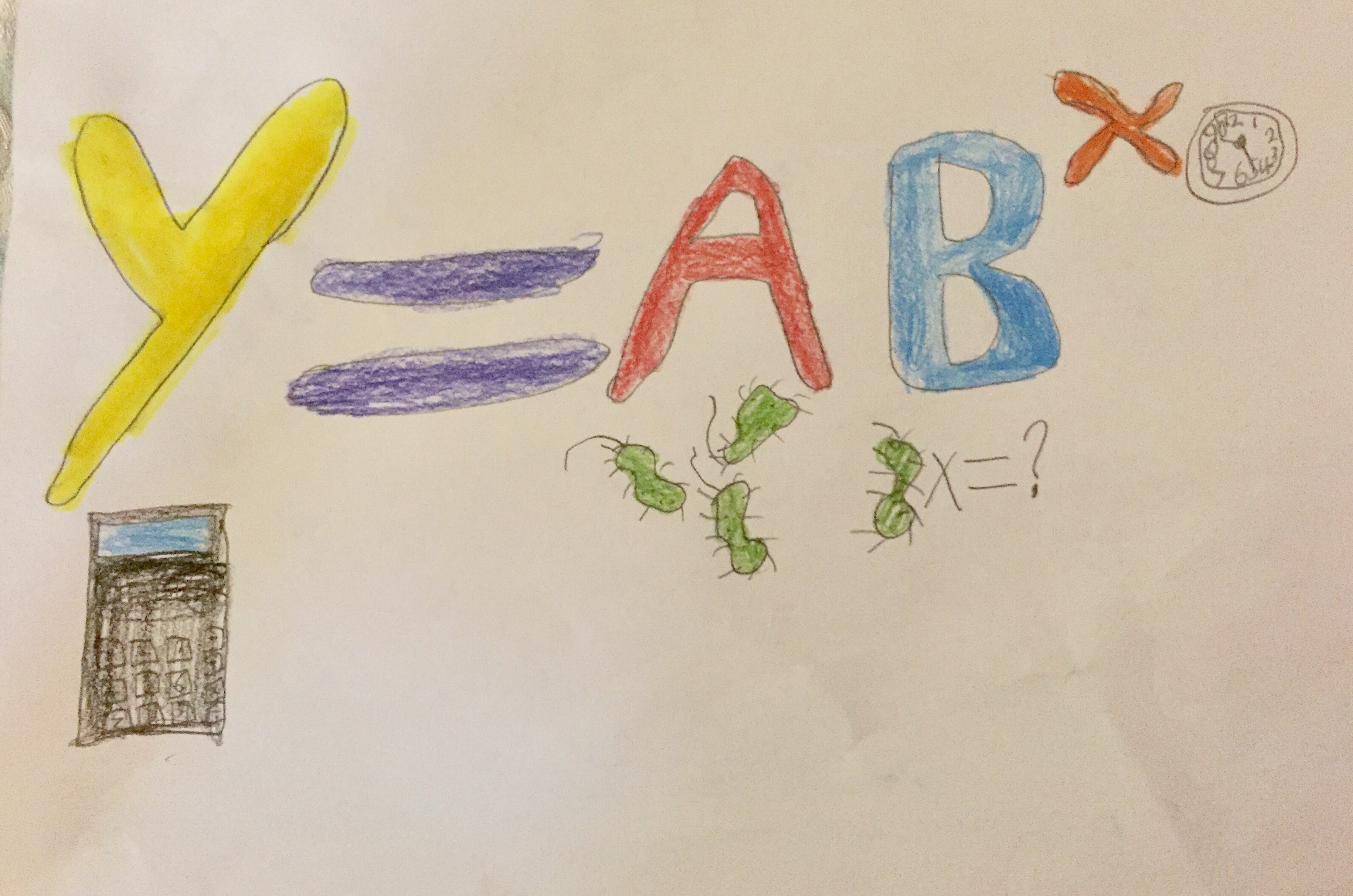
I noticed that after this exercise, students were beginning to talk about the formulas by identifying individual elements and their actions. When explaining why representational items were chosen, students were recalling examples from word and story problems from our practice work.
Research (source articles noted below) shows the value of connecting the abstract ideas of math to concrete items and has been proven to help with retaining the material. In this lesson, connecting physical objects (or in this case, drawing pictures of physical objects) allowed my students to make clear connections to what the formula was representing. More than that, this exercise functioned as a valuable informal assessment for me about what my students really understood about the elements and actions of the formulas we were learning. I look forward to using this task again!
Research that supports connecting concrete and abstract ideas: Allsopp (1999); Baroody (1987); Butler, Miller, Crehan, Babbit, & Pierce (2003); Harris, Miller, & Mercer (1993); Kennedy and Tips (1998); Mercer, Jordan, & Miller (1996); Mercer and Mercer (2005); Miller, Butler, & Lee (1998); Miller and Mercer, 1995; Miller, Mercer, & Dillon (1992); Peterson, Mercer, & O’Shea. (1988); Van De Walle (2005); Witzel, Mercer, & Miller (2003).
Pre-preplanning
School officially starts back for my district on August 6 this year. Before that happens, teachers gather. Today and tomorrow some teachers from my math department are gathering even earlier. We will take two days to fine tune our plans, to collaborate, to build a bit more strength into our teams. Next week begins the official preplanning. The agenda is set. About 6 hours of the five days has been designated for curriculum teamwork. We’ll take it now, early. Next week will be quite busy enough.
I am ending my summer a little bit early. Why? Because I want my students to have their best year ever, and I’m going to plan for it!
Our curriculum team makes this possible through pre-planning grants that are available through Title I funding. To find out if there are funds available at your school, check with your county’s Title I coordinator!
Asking the right questions of ourselves…
We question our students to elicit and engage, to push their sensemaking, to activate prior knowledge, and to get them thinking about their thinking. But do we question ourselves and our pedagogy with the same focus?
Table taken from National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all.
In the rush to use new ideas, incorporate technology, or just ensure our students are doing math things from the minute they walk through the door, are we giving enough thought to why we are choosing an activity? What is that activity suppose to achieve? Has it earned the time it will take, not only for the students to complete, but for the grading and feedback? In other words, will it move these students further towards the goal?
Learning Targets are Not Just For Kids
My colleagues and I have been asked to share learning targets with our students; to write the daily lesson or goal on the board and go over it, so students know what successful learning looks like.
As you think about what your students will be doing, do you ask yourself just how the activity will provide the experience you want for the student? What will it tell you or your student about their learning? How will it move them closer to understanding? How will it engage the learner to produce the desired result? What will the failure of this activity tell you? Tell your student?
For the math classroom, skill builds upon skill. Knowledge is formed by understanding how the old can be reshaped or used to fit into the new. It’s like reading, but with numbers. In learning to read, we begin to decode shapes that are letters, that make sounds, that can be arranged into words (patterns of letters), that are then arranged into larger groups of sentences to convey information.
In mathematics, we learn our numbers, which instead of sounds convey amounts. At first, these amounts are concrete, as we count fingers or toes or toys or blocks or cheerios. At some point the numbers begin to represent the amount. We put these numbers together into groups that define patterns, and we put these patterns into sentences that convey information. Every time we learn a new concept, we can place that building block in context and do more than we could. A concept in math means we’ve identified a relationship, a cause and effect, a reasoning about how one action effects an outcome. When we understand the connection, we can extrapolate, interpret, compare, contrast, synthesize, and create. All of those things that we say we want our students to be able to do, no matter the subject.
Is this what your materials and lessons are teaching?
Every teacher reading this has bemoaned the lack of time we have in the classroom. How we spend that time often forces us to cut our activities, explorations, and conversations about the material. We have to hit the ‘most important’ standards, or the ‘big ideas’. Yet we know that knowledge is built by exploration, by focusing on a problem or situation, by playing with ideas. But how often have you asked ‘how will this activity increase understanding of the concept?’ ‘What is it teaching?’ ‘How does it allow showing the learning, or mastery?’ ‘Will it allow for connections to what has already been done, or to what is to come?
Is the idea or activity sticky?
By sticky I mean will this be something the student will think about longer than the activity itself. Will a student come in a day or a week or a month later and say, ‘I’ve been puzzling about this idea and I think I finally get it.’ And yes… I believe all of our ideas can be sticky – not necessarily for everybody at the same time. If we are truly giving each part and moment of our lesson thoughtful care, there will be more sticky moments than not. Those moments are what build interest, knowledge, and understanding. One of the best examples of this is the Four Fours activity. My students worked on that for over a week!
How do we get there?
1. Put yourself in your students’ shoes.
Think about what is happening to them daily. When they walk into your class, where are they coming from? Have they had time to process their last class? (Probably not.) Are they looking forward to math or dreading it? Did they do their homework – or even understand it? Is your class a relief, a chore, or an interesting, thought provoking space in their day? As I write this, I see the faces of my students, and can easily see the few that truly look forward to this class – but there are occasions where my lessons have let them down, too!
What do they need from you in that moment, to get their mind off of what has happened up to the moment they walk through your door?
For a start, pretend you are a student and walk into your classroom. Pick up that starter. Take it to a desk and try your own lesson. Where is your student brain? How does it make you feel? Does it do you want it to do? Loosen them up? Assess yesterday’s lesson? Review a skill they need in the main lesson? How will you check the outcome? This shouldn’t be a ‘take up and grade’ – it’s very name implies short, sweet, and to the point. What you want to accomplish must guide what you do. What you do sets the tone for the rest of the class. If the starter isn’t working for you, it isn’t working for them. Stop. Just stop doing what doesn’t work.
One teacher I know
has a great routine. She has trained the kids to pick up a starter (half page, every day) on their way in. Some fill it out. Some don’t. She goes over each problem, quickly working it on the board. She asks a few questions about the numbers or the process. Usually she has to get the class’ attention, many are off task. The kids who knew how to do this are already zoned out. The ones who don’t know how either copy her work down exactly, or don’t write anything. She does this quickly, and in her mind this is circling back around as a review for weak skills or concepts. She is practicing good classroom management by getting kids in their seats and working. She has trained them that math is boring.
During one week, she gave the same material as a starter and as a quiz to check for Learning. To her frustration, it did not result in increased knowledge for those who hadn’t already learned it (and I suspect it was extremely boring for the handful who did!) This is a 15-20 minute activity every day. How could she change this activity to get the desired outcome, i.e. strengthening this skill?
2. Ask yourself what your lesson is teaching: Process or Concept?
A process is a pattern of activity. A concept is the explanation or reasoning for why we do the process. Teaching a concept should lead to the process. In the interest of time, students often learn the process. Then it’s practice, homework, and a test. Are you teaching process or concept? Are you reviewing process or concept? Are you practicing process or concept? Concept is harder, takes more time and doesn’t work well on a worksheet. It is much more interesting, however. Concept is sticky.
You do not have to reinvent the wheel!
No time to write those magnificent lessons? Have I got a tip for you! You do not have to do this alone! Lessons and resources are out there and so many are FREE. Check out these links (courtesy of Matt Vaudrey and the #MTBoS:
Not only will you find good lessons, you will find teachers who are constantly looking for better ways to share this wonderful world of mathematics!
Here are a few more questions for you to consider, (and which I will be grappling with while planning my next classes):
3. What is my lesson intended to do? How do my materials (problem set, delivery, class activity and structure, timeframe, sensemaking, etc) support this goal?
4. Where are my kids likely to fail? What can I do beforehand to support the weak spots (Starter idea!)?
5. What does the learning of the concept look like? What do I do for those that ‘get it?’ What do I do for those that need more? How will I know (formative assessment). If they don’t start, WHY not? If they don’t finish, WHY not? Do they really know how to do it? Is homework appropriate- i.e. will this truly extend the learning?
6. Does my lesson connect this idea to what they already know? Does it give them a peek into a future idea?
7. When/how will I give them time to process what they’ve done?
8. When will I revisit? How will I revisit? (Yes! Plan for this!)
I leave you with this:
The moment you can really know a student has internalized a concept/learning target is the moment you hear/see them sharing what they’ve learned with another student. Plan for that, too.
Change the mindset from ‘finished’ to ‘learning’….
In this continuing exploration of Academy high school practices and their unique position to affect change, the idea of changing classes every day, every hour or more, is examined.
Currently, the Academy school model is some type of block schedule. Students take an assortment of courses in order to meet a specified list of credits towards graduation. Throughout the day, students get an hour to 90 minutes of a subject, bells ring, brains shift, and the activity is repeated over and over, until the final bell. Is this really the best way to learn? Is it the way we learn to tie our shoes? Did mom give us an hour of this and an hour of that as we learned to make cookies, or learn that different sized pans would only hold so much, before spilling the contents across the floor? Did a timer go off somewhere as mom yelled that it was time to go learn something else?
I believe there is a better way. We learn by experiences: examination of a situation, trying a solution, evaluating the result, trying again, evaluating, reflecting, etc. and throughout the process, storing the experience for future reference. There is also an element of sharing, talking over results with another person who has experienced, or is experiencing the same thing. With my students, however, I usually get one offering a solution and the other copying it down, in order to simply get finished. No learning, because the goal isn’t to learn. The goal we’ve set is for them to get ‘finished.’
Change the mindset from ‘finished’ to ‘learned’ or ‘learning’ and time becomes irrelevant. The goal is learning, so students don’t leave (or they return each day) until they’ve mastered the concept.
The idea that students are given a list of items to accomplish at the beginning of their high school career, and that they can finish them in any order, and in whatever time frame they are able, is a concept whose time may have come.
What if high school were as exciting and looked forward to as coming of age? Shouldn’t this be a time of discovery and promise, instead of dreaded and scary? To give our students the responsibility of their own learning, I believe they also need to know what that learning entails, so they are properly equipped to run with the responsibility!
I think it is time we return to trusting our kids with more, sooner. The movement to protect kids has pushed personal responsibility to the back burner. We are so afraid of letting kids fail, we do things for them, which creates a child that doesn’t need to step up and take responsibility. In addition, it creates a child that views failure as a disgrace, meaning that child will do everything in their power to avoid failure. I’ve observed students who work harder to avoid failing – often by cheating or straight up avoidance – than they would to engage in the learning! In their defense, the classroom can be a real snoozer if there is nothing engaging or relevant going on.
‘I believe every child can learn’ is the new mantra.
What I don’t see is the belief that every child can take control of their learning; that we can trust natural curiosity to take them places our planned lectures never could or will. There has to be a freedom on the part of the teacher to ‘hang on for the ride’, as the student forges ahead.
It’s a little like taking a horseback ride.
Every student has a mentor, advisor, or adult that holds them accountable. The entry to high school is planned in a community of parent, student, teachers. The goals for the learning are spelled out. The reins are placed in the child’s hands, with guidance. The adults are the spotters, close in the first few rides, backing off as the student gets more familiar with the process and expectations. The student isn’t being pulled along the path to the destination; the student is choosing the way, enjoying the ride, the pace, the view. The destination arrives naturally, and perhaps a little differently than first envisioned.
This idea does require a bit of a structural change. Instead of a class schedule, a school could end up with every student starting in the same place! Big room needed! The solutions could involve everything from an orientation style of instruction with starting points, to letting students come up with possible solutions that would allow them to get in the knowledge- and learning time- they need.
The Checklist
So what does this checklist look like? Is it the same for every student? Is it modifiable, like college programs? What’s required? What’s negotiable?
Is it a list of standards, or more a list of abilities, attitudes, or problem solving? Is it a bit of both? How do we assess the learning? Who assesses the learning and levels of achievement?
This process requires collaboration among student, parent, and faculty… but it also requires a commitment on the part of teachers and school leaders to stick by the rules: student choice, student struggle (a critical component), and a plan to reward success AND failure, because there will be both, if we’ve done it right. It’s time to do this right, and to return a love and excitement for learning back to our children!
Academy schools are uniquely positioned for changing the landscape of education.
The first day of 9th grade. DaiCrede is very nervous. He’s heard about this high school, just rumors of course, that they let you choose what you want to learn about, there are no regular classes; you work with teachers in each area as you need the information to complete your project. There aren’t grades, just levels of achievement for learning targets. He’s not sure if he can make it in this environment. He is excited about the robotics lab, though. That would be cool…
Shelly can’t wait for the bus to get her to school today. She fingers her Advances in Analytical Chemistry magazine. Finally, a school that will let her pursue her dream of becoming a medical researcher! Just think, a whole day devoted to learning how to run a research program. No breaking the day into language, math, history! She can grab those things as she needs them for her project. She loved meeting with her teacher mentor during the summer to set up her project parameters. She’s nervous and ready.
Ned is nervous, too. He rides his bike, slowly circling the parking lot. High school. He’s not sure how having no classes is gonna work. How will he know what to do?
First Week: Orientation
This Academy High School has a Ninth Grade Academy for incoming freshmen. They will be going through a series of workshops this first week to learn how to navigate the process. By the end of week two, they’ll have chosen an initial Academy. During the third week, they’ll have chosen a project and have begun breaking their project into tasks – and identifying the various areas of knowledge they’ll need to access. They won’t go it alone, however. All students have been assigned two mentors: a teacher, and a student from a higher grade, (Mentoring is a learning target for all students, more on those later) who will help them navigate the project system and hold them accountable for task goals and deadlines. While this may not feel like a structured environment, there is a definite structure and protocols. The flexibility comes in as each student is allowed to follow his or her interests, change from one Academy to another as they explore, and begin to search out what they need to know as they need it. There is a framework for that!
That first week will see new students rotate through a series of workshops and learning sessions on the School’s Academies. These new-to-high schoolers get information on the various fields of study available to them. (Students may have chosen to come here- if their zoned high school is not an academy school, or if they were not doing well in a traditional school setting). Returning students share their experiences with the process about to be undertaken; what worked, what they liked, what they found most challenging, what they would do differently. They testify to the powerful learning that takes place when they were able to choose topics for study that they wanted:
“Math becomes relevant when I had to figure out what was happening in my chemistry experiment. I went into the math room, laid out my work, and asked for help. Once we started, I realized I didn’t know the basics. I spent two weeks in the math lab, working through background knowledge, then learning how to apply it to my research. Whenever I got stuck, I would go back and get help.”
“I had to write up a report on my project. The requirement that it be a formal paper, with citations and everything was overwhelming. I didn’t know how to do that. I had to spend that last month in the English lab. I wish I’d started there first! Everything I had done was in this big pile of notes. I had to learn how to write, how to make coherent paragraphs that made sense to others. I must have rewritten my summary statement a million times before I wrote my first draft. It was hard work, but I wanted to submit it to the robotics journal. I didn’t want to be embarrassed.”
“I have always wanted to go into nursing. I got to plan each of my 9 week projects around a different area of nursing. At first, it was hard to stay on task. I didn’t have to do anything but show up. I would log in to the electronic attendance monitor and consult my task plan. That plan kept me on track with assignments. If I didn’t know how to do something, I would go to a lab and get help from the teachers. It’s really different; me asking them what I need to know, instead of them telling me what I was going to learn that day.”
“The projects seem really hard. There is so much to do, it’s overwhelming. That first project is really where you learn how to do everything. The first few weeks of high school, you learn about the academies and you are encouraged to pick your project. There are lessons on how to break down your project by tasks. I took a quiz to find out what I was interested in for my first project. Some kids come in knowing what they want to do. I wish I had gone to the summer workshop. I could have started my project so much sooner!”
“My mentor teacher was a big help. He ran one of the math labs, but he always had time for my questions. When I felt like quitting, or when I would hit a wall in my project, he would let me talk it out. He listened, really listened, to me. As a sophomore, I’ll be completing two projects, instead of four. I’ll need a team of students to meet the advanced requirements. I’ve made some new friends on this last project that are in my Academy. I think we’ll work well together.”
“The best part of my project, water resources for our community, was presenting what I had found out to the local water board. I had some suggestions for making our water supply healthier, with the project costs and a timeline for implementation. My next project will be on finding a new way to deliver water to neighborhoods. Seems to me there has got to be a more resourceful way than digging and burying pipes in the ground!”
“I graduate tomorrow. I’ve already got a starting job in a large engineering firm. I was able to intern with them as a result of a project I chose during my freshman year. That led to another project during my sophomore year. My junior year, I got a small grant to research affordable housing – after I learned about writing grant proposals in the English lab. One of my projects was on making presentations to community developers, which I used to apply for the job I’ll be going to after high school. They were impressed with the amount of experience I’d gained in researching and development of my projects, they liked my presentation skills, and they will help me pay for my engineering degree while I work for them!”
Learning Targets are the New Standards for Career, College Readiness
Teamwork, innovation, self-motivation, serious work ethic, honesty, integrity, and getting paid for something we love doing are some serious life/work goals. The Learning Targets replace standards by giving students real, usable skills for life. Critical thinking is absolutely necessary for making sound decisions. Being able to communicate through written, visual, or verbal methods is a must. These, and more Learning Targets, are imbedded in every project outline. Each year, the project should add appropriate learning targets, building on prior years. And who says a student must take four years? An Academy school has the ability to let a student move more quickly towards a goal, be it work or college. In addition to the projects, which can increase in complexity for those pursuing two, four, or six year collegiate or technical degrees, there are technical and apprenticeship projects and programs that would fit cleanly into this model, allowing our students to investigate different types of jobs through projects, and interact with the community during their research, giving them an authentic audience – the best way to incorporate honest evaluation, and spur our kids’ interests in their futures.
I work in an Academy school. I believe in this scenario, and I believe our students would be more than willing to embrace – and benefit – from this new way of looking at their education and preparation for life.
I see a couple of things (and will probably think of more!) that would need to be done:
1. Start with the 9th grade, move up with them. Don’t try to change all four grades at once. Set reasonable learning targets for them, understanding that this replaces the 9th grade standards. Build in what they need to know in each project. These won’t be lightweight! Each project must take each child through the four core fields of history, science, language arts, and math, incorporate electives such as art, physical activity, technical (computer) or programming…. but it’s OKAY if some projects are heavier in one area than another. They will be completing four projects across the year. I think this mindshift on the leadership will be the hardest!
2. Train the teachers. Take two-three weeks to train your teachers in the Learning Targets and what mastery of these Targets should look like. Teach them how to facilitate the labs, because they won’t be teaching specific, planned lessons! Teach them the framework tasks of the project- so that no matter what the child chooses to learn about, all tasks from the framework are applied. For example, a child wants to learn about yo-yos: there would be tasks to learn the history, find the financial impact of the toy, write their findings in an essay with citations, consider the making of the toy, the science behind the motion of the toy, the aesthetics, or traditional design and decoration of the various models,perhaps the value in an exercise program, and how it could benefit the user. This is a do-able 9 week project for a 9th grader.
3. Inform the parents. Teach them what is changing. Tell them what we are looking for in terms of benefits. Give them the long view. Give them the questions we want them to be asking through the process, so they can feel, and see, their child growing and learning through the process. Create parent buy-in at the start.
4. Tell the kids, in middle school, what is happening, what we want for their future, what will be required of them. Give them a chance to go to a summer workshop, where they can investigate what their interests are, a short survey, some simple practice on picking topics, a brief look at the project tasks framework, what the labs will look and feel like, how to approach teachers and ask for help.
There is more, but I think this is a big enough chunk to chew on for today. Your constructive thoughts are welcome!
L-Q-E vocabulary (or how to drive your OCD students crazy!)
Algebra I, Unit 5, Compare and Contrast Linear, Quadratic, and Exponential functions…
This simple vocabulary lesson generated a surprising result: my kids thought the end result was too messy, so many of them didn’t want to follow the final step!
The activity uses a simple alphabet mind map. It is a 5×5 grid with a letter of the alphabet in each square. The last square contains X and Y. You can print a copy here, or have the students draw their own.
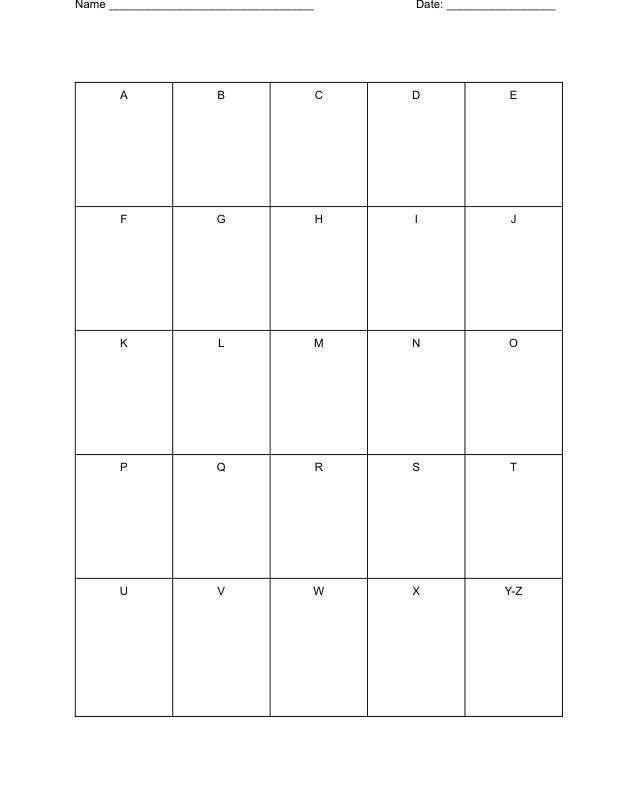
The standards for this unit were that students should be able to identify linear, exponential, and quadratic functions from equations, graphs, tables, and contextual situations, and be able to compare each function with regard to rates of growth.
To achieve these skills, students needed to be able to identify the key characteristics and key vocabulary associated with each type of function. They also needed to be able to discern small differences in equations, the shape each functions takes when graphed, and the changes in a table that would indicate what type of graph the table would produce. Given contextual scenarios, they needed to identify which type of situation would produce a linear change, a parabolic track, or a classic J-curve from exponential growth or decay.
When we started, they could barely list the key characteristics, much less identify which function was associated with each characteristic, what those characteristics looked like, or how to tell them apart. They needed stronger, more fluent use of the vocabulary!
Step One, The challenge: using each letter of the alphabet, fill in the grid with the names of as many key characteristics of each type of graph as each student could think of. (We’d made lists over the previous several days, along with examples, so I knew they would be able to come up with several familiar words.) I encouraged them to start with any word they could think of that they associated with graphs or equations. As they wrote, I then passed out colored pencils for the second part of the task.
Step Two: After about 10 minutes of individual work, we came together in a large group, and I asked each student to share one item from his/her list. I encouraged the students to add new words they heard to their papers, and to use a different color pencil than they used to write their initial lists. After going around the room about two times, we asked kids to popcorn choices that they had on their papers that hadn’t been covered. We had a few letters that remained without words, so we again asked for ideas from the whole group that would fit for those letters, reminding the students to stay within the linear, quadratic, exponential, and graphing parameters.
We found that we had to ask a few thought provoking questions to make sure some important terms weren’t left out.
(At this point, because we were talking about why these words were acceptable, what they meant, and how they were related to LQE, I had a pretty strong idea of where my kids needed additional help and lessons!)
As my students shared their words, I wrote them on a poster sized alphabet chart that I had prepared beforehand. I gave the students a few moments to make sure that they copied all the words from the collaborative chart onto their personal charts.
Step Three: each child labeled the outside of their chart with the words LINEAR, QUADRATIC, and EXPONENTIAL.
I explained that we were now going to match each term with the function to which it belonged by drawing a line from the word to the function. I warned them that some words might belong to more than one function!
They each picked a color to use for the line that would connect the appropriate words to LINEAR. The first word under A, asymptote, was determined to be related to exponential, not linear. Not only did they have to decide which function, they had to say WHY and in what way the word connected with FUNCTION. The word Axis was next. Everyone could get behind that as a graph term that could belong to any of the function types, but we only connected words to one type of function at a time. We would come back to ‘axis’ two more times as we matched words with the other two functions! Colored lines were drawn from Axis to LINEAR. This happened with several more words, before the students began to realize this was going to get messy. I was drawing the same lines on my big poster, but I was totally surprised as students began color coding each word with dots, or making these neat lists on separate pieces of paper, sorting out each of the characteristics, because they didn’t like the tangled mess that was happening on my poster. (I explained that they were actually drawing the map for their brain, not their eyes. They were somewhat skeptical…). ‘I can’t read it,’ was the standard response!
I encouraged the students to use a different color for each category, and we progressed in order through each function, so no one would end up confused. Throughout the matching, as students popcorned answers regarding which words to connect, I continued to ask for agreement, disagreement, (thumbs up, thumbs down) and ‘why, how do you know,’ from the whole group. This was a very intense, fast paced portion of the activity, with even some of my most blasé students getting involved!
We followed this activity with a neat card sort, that was another intensive activity in and of itself, and was spread over two days. By the end of these activities, I could tell that more of my students were fine-tuning their selection processes, looking more closely at the details of each equation, graph, or table, and applying the key characteristics lists they’d made to their compare and contrast process!
Here were some lists they made of the key characteristics:
Close Reading in math; and the “after” math…
Literacy is everywhere, including math class. And I don’t mean those clever (and not so clever) word problems.
I used a simple story book, predictions, and paired discussions for my 9th grade Algebra I -ers. I passed out colored pencils for annotation, and paper for predictions.
We started with the brief prelude, a paragraph, about a ‘happy-go-lucky young man’ who meets an old man who tells the young man,’I have a gift for you.’
There were a few other clues in the paragraph, so after asking the kids to read and annotate the paragraph individually, a volunteer read the paragraph aloud. With no further discussion, I asked each student to write down their prediction of what the story was about. Then I asked them to share their predictions – and their reasons why they thought that – with a partner. Then they would listen to their partner’s prediction and decide if they agreed or disagreed.
I modeled having a conversation…
To remind them of how to have a meaningful conversation, I modeled listening, responding with questions about what was said, and commenting on the information. We talked about how conversations were about listening and responding, not a contest of spouting information. Everyone got to practice, with a little (okay, a LOT of,) prompting!
We turned to page 2. My students were now eager to read further (we had predictions to fulfill!), and since the book’s format was laid out in sections of two to four sentences, with lots of images, I was able to let all have a turn. We took the four sections on pages two and three rather slowly, and we pulled apart the actions of the old man (he gave the boy two seeds), and the young man (he cooked one seed and planted the other seed). We talked about the passage of time – winter, when they had met, and the boy planted the seed; spring as the ‘sturdy’ plant appeared from the ground; summer, when the plant produced two flowers; and fall, when two fruits became evident. Each one of my questions caused them to return to the text for details.
Before we turned to page four, I asked my students about their predictions, and whether they had changed their predictions based on this new information. The conversation among the students turned to the details they just reviewed: how long it took to grow the seeds, how one seed could feed someone for a whole year, and why couldn’t he get food where he lived. New predictions came from the ashes of the old, with several students predicting that the plant would grow huge, up to the sky, and the boy would climb it. This was an obvious scaffold onto a familiar story. They told me the key word ‘sturdy’ meant that it would be strong and big. We turned the page.
New predictions came from the ashes of the old…
As each student read a section, we learned that the plant the young man had grown produced two more seeds from the fruit. He cooked and ate one and planted the other. We noticed from the picture that he put a hammock in a tree. Apparently he was planning on staying put. I pointed out that this was something that usually happened when people planted, instead of hunting for food. Another scaffold, as they agreed with me that he would need a place to sleep while the plants grew.
Again, we turned the page. This time, the readers learned, Jack (that was the boy’s name) had managed to grow another plant from the seed, which yielded two fruits, which yielded two seeds, one which was dutifully cooked and eaten and one planted in the ground. No changes here, but we noticed in the drawings that Jack seemed to be getting fat. Also, the plant wasn’t getting any bigger, which some of the boys seemed disappointed with. I think they were still waiting for the plant to grow up to the sky. One boy persisted in asking why Jack just didn’t move to a place where he could buy some food. We made more predictions, adjusting our expectations based on what we’d read. I asked them if their mental picture of the story, and of Jack, was changing. One of the girls agreed, and then we turned the page.
Their mental picture of the story, and of Jack, was changing…
The next two pages supported the story line. Jack continued for two years to cook and eat a seed and plant the other. The plant never got any bigger and never produced any more than two flowers, two fruit, and two seeds. It looked as though Jack would be living out his life, year by year, cooking, eating and planting seeds. I had the students make predictions anyway, and talk about what they thought Jack should do, given the circumstances. Some of the children thought Jack was stuck in a rut. On to the next page…
My readers were still eager to read. They continued, aloud, to devour the slim text (it was great to get a window into their abilities to read and decode the text – you know, for those word problems we will get to someday!) It was momentarily exciting to hear that Jack was as bored with his existence as some of my students! He said, and I am paraphrasing here, ‘if I always do what I have always done, I will never get anything different than what I’ve gotten.’ (Here I looked at my math students to see if they had taken anything of a personal nature from this comment. It appeared they hadn’t felt a connection.)
‘What,’ I asked, ‘Do you think he is going to do?’
‘He’s going to plant both seeds,’ spouted one girl. ‘But what will he eat while he waits for the plant to grow?’ I asked. They hadn’t thought about that, and in thinking about it, several students were seriously confused about how many seeds he could plant if he ate one, and he only had two to start with. (This may point to a reason that so many students struggle with adding negatives and positives.)
A serious discussion ensued as to what he was giving up if he didn’t eat the seed. Would it be worth it? We talked about how sacrifice is sometimes needed to affect change. One of the kids said he would be cranky because he was hungry – the voice of experience talking? The kids had gotten into the spirit of the lesson and were ready with their predictions. The Jack and the Beanstalk contingent were ever hopeful. There was still one boy who wanted to know why he didn’t just move to a place with food and forget about the seeds. We turned the page.
The story continued with Jack explaining that he decided to go hungry so he could plant two seeds. To assist the verbal process, and give structure to the next round of predictions, I drew a table on the board and labeled the two columns ‘seeds planted’ and ‘seeds produced’. I then filled in the first line. Under ‘seeds planted’ I wrote 1, and under seeds produced, I put 2. I asked the kids to review the current situation: is this correct so far? After some discussion of my column titles, the students agreed. I asked them to fill in the next line. Now that Jack has decided to go hungry for a year, how many seeds will he plant? The students agreed he would plant both seeds.
I wrote a 2 on the second line under ‘seeds planted’.
‘So what goes under seeds produced?’ was my next lead in, ‘and why?’
Another look at the text produced the facts: two seeds produced two plants, each with two seeds. How many different ways could we count this, and still get answers varying from 2 to 6?!?
More fingers, more math. One girl supported her position loudly by mentioning multiplication; two plants times two seeds would be four. Several students had made the same conclusion by different routes, but getting the kids to share their explanations that they had discussed with each other was the hard part. The confidence that they can be right is so difficult to encourage! The student who mentioned multiplication was encouraged as another student agreed with her. A 4 was written in; satisfaction all around.
So, how many seeds will he plant next? And ‘why?’
‘Four’ was the immediate answer, until a single student voice reminded us that he had to eat. So began another discussion about how to calculate the number of seeds, and how many will he eat, and how many will he have to plant? Some students felt he was going to eat two of them. (We had doubled the amount of seeds grown – we must double the amount he could eat!)
We returned to the initial instructions on page 1. A student read the evidence and told everyone definitively that only one seed would feed Jack for a whole year. By this point, I was listening to these children teaching each other how to support their facts, correct their misconceptions, and expose and correct mathematical errors. Every child was involved in this discussion – every child!
One seed eaten, three seeds planted was the ultimate conclusion. (If I rendered their discussion here, you would be as bored as we were with three years of Jack eating a seed and planting a seed!) The chart was filled in, and we were ready for the next question: if he plants three seeds, how many seeds will he have to plant the next year?
While the whole process was a conversational struggle, before I left them to this final prediction, I pointed out the table and had them write it in with their predictions. We had just begun defining a function the day before, so I asked them if they thought this was a function? I was rewarded with a student identifying the input and output terms of seeds planted and seeds grown, as x and y. Several students then made the next connection to the fact that none of the inputs we had so far would repeat, so it must be a function.
Without giving away any more of the story, I will tell you that they were able to successfully calculate the answer. We stopped here as I had them make a final prediction about the rest of the story. We will revisit Jack and his adventures in the coming unit.
Here is the ‘after’ math:
Our school lit coach came by two days later and interviewed some of the students that had participated in the close reading. Here are some of their comments (I stayed across the room, out of their line of sight. I was curious to hear their honest responses.)
- “I liked it because it was different from the way we usually do math.”
- “Why can’t we do math like this all the time?”
- “I felt like I really understood the story.”
- “I remember more about how many fruits Jack planted.”
- “The table helped me understand.”
- “I think it will help me in my reading in other classes.”
Read that last bullet again.
‘I think it will help me in my reading in other classes.’
Wow. Now, that’s some kind of ‘after’ math!
Editor’s note: the standards for this lesson had to do with identifying functions; recognizing a function in multiple forms (such as tables), identifying functions from contextualized settings; the literary standards were identifying supporting information and using contextual clues to support mathematical arguments (a Mathematical Practice, as well). Additionally, the conversation supported mathematical reasoning, practicing vocabulary, and reasoning aloud. The constant predictions were embraced by the students, who stayed involved for what amounted to about 60 minutes of close reading. They had to know each outcome! No one read ahead, which surprised me a little. They really wanted to maintain the suspense! I can’t wait to revisit Jack and the rest of his story!
For those who notice the reading level, I wanted to use a text that would provide a low floor, and that would allow me a high ceiling – the actual math is writing and calculating an exponential equation. This was a great text for my ninth graders! The text didn’t cognitively get in the way of the activity.
To read Jack’s full story, visit Anno’s Magic Seeds, by Mitsumasa Anno. For more of her series of math books click here.
One of Thirty Voices 