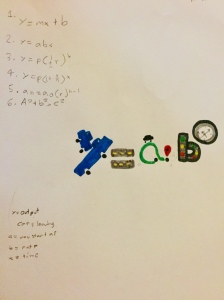Literacy is everywhere, including math class. And I don’t mean those clever (and not so clever) word problems.
I used a simple story book, predictions, and paired discussions for my 9th grade Algebra I -ers. I passed out colored pencils for annotation, and paper for predictions.
We started with the brief prelude, a paragraph, about a ‘happy-go-lucky young man’ who meets an old man who tells the young man,’I have a gift for you.’
There were a few other clues in the paragraph, so after asking the kids to read and annotate the paragraph individually, a volunteer read the paragraph aloud. With no further discussion, I asked each student to write down their prediction of what the story was about. Then I asked them to share their predictions – and their reasons why they thought that – with a partner. Then they would listen to their partner’s prediction and decide if they agreed or disagreed.
I modeled having a conversation…
To remind them of how to have a meaningful conversation, I modeled listening, responding with questions about what was said, and commenting on the information. We talked about how conversations were about listening and responding, not a contest of spouting information. Everyone got to practice, with a little (okay, a LOT of,) prompting!
We turned to page 2. My students were now eager to read further (we had predictions to fulfill!), and since the book’s format was laid out in sections of two to four sentences, with lots of images, I was able to let all have a turn. We took the four sections on pages two and three rather slowly, and we pulled apart the actions of the old man (he gave the boy two seeds), and the young man (he cooked one seed and planted the other seed). We talked about the passage of time – winter, when they had met, and the boy planted the seed; spring as the ‘sturdy’ plant appeared from the ground; summer, when the plant produced two flowers; and fall, when two fruits became evident. Each one of my questions caused them to return to the text for details.
Before we turned to page four, I asked my students about their predictions, and whether they had changed their predictions based on this new information. The conversation among the students turned to the details they just reviewed: how long it took to grow the seeds, how one seed could feed someone for a whole year, and why couldn’t he get food where he lived. New predictions came from the ashes of the old, with several students predicting that the plant would grow huge, up to the sky, and the boy would climb it. This was an obvious scaffold onto a familiar story. They told me the key word ‘sturdy’ meant that it would be strong and big. We turned the page.
New predictions came from the ashes of the old…
As each student read a section, we learned that the plant the young man had grown produced two more seeds from the fruit. He cooked and ate one and planted the other. We noticed from the picture that he put a hammock in a tree. Apparently he was planning on staying put. I pointed out that this was something that usually happened when people planted, instead of hunting for food. Another scaffold, as they agreed with me that he would need a place to sleep while the plants grew.
Again, we turned the page. This time, the readers learned, Jack (that was the boy’s name) had managed to grow another plant from the seed, which yielded two fruits, which yielded two seeds, one which was dutifully cooked and eaten and one planted in the ground. No changes here, but we noticed in the drawings that Jack seemed to be getting fat. Also, the plant wasn’t getting any bigger, which some of the boys seemed disappointed with. I think they were still waiting for the plant to grow up to the sky. One boy persisted in asking why Jack just didn’t move to a place where he could buy some food. We made more predictions, adjusting our expectations based on what we’d read. I asked them if their mental picture of the story, and of Jack, was changing. One of the girls agreed, and then we turned the page.
Their mental picture of the story, and of Jack, was changing…
The next two pages supported the story line. Jack continued for two years to cook and eat a seed and plant the other. The plant never got any bigger and never produced any more than two flowers, two fruit, and two seeds. It looked as though Jack would be living out his life, year by year, cooking, eating and planting seeds. I had the students make predictions anyway, and talk about what they thought Jack should do, given the circumstances. Some of the children thought Jack was stuck in a rut. On to the next page…
My readers were still eager to read. They continued, aloud, to devour the slim text (it was great to get a window into their abilities to read and decode the text – you know, for those word problems we will get to someday!) It was momentarily exciting to hear that Jack was as bored with his existence as some of my students! He said, and I am paraphrasing here, ‘if I always do what I have always done, I will never get anything different than what I’ve gotten.’ (Here I looked at my math students to see if they had taken anything of a personal nature from this comment. It appeared they hadn’t felt a connection.)
‘What,’ I asked, ‘Do you think he is going to do?’
‘He’s going to plant both seeds,’ spouted one girl. ‘But what will he eat while he waits for the plant to grow?’ I asked. They hadn’t thought about that, and in thinking about it, several students were seriously confused about how many seeds he could plant if he ate one, and he only had two to start with. (This may point to a reason that so many students struggle with adding negatives and positives.)
A serious discussion ensued as to what he was giving up if he didn’t eat the seed. Would it be worth it? We talked about how sacrifice is sometimes needed to affect change. One of the kids said he would be cranky because he was hungry – the voice of experience talking? The kids had gotten into the spirit of the lesson and were ready with their predictions. The Jack and the Beanstalk contingent were ever hopeful. There was still one boy who wanted to know why he didn’t just move to a place with food and forget about the seeds. We turned the page.
The story continued with Jack explaining that he decided to go hungry so he could plant two seeds. To assist the verbal process, and give structure to the next round of predictions, I drew a table on the board and labeled the two columns ‘seeds planted’ and ‘seeds produced’. I then filled in the first line. Under ‘seeds planted’ I wrote 1, and under seeds produced, I put 2. I asked the kids to review the current situation: is this correct so far? After some discussion of my column titles, the students agreed. I asked them to fill in the next line. Now that Jack has decided to go hungry for a year, how many seeds will he plant? The students agreed he would plant both seeds.
I wrote a 2 on the second line under ‘seeds planted’.
‘So what goes under seeds produced?’ was my next lead in, ‘and why?’
Another look at the text produced the facts: two seeds produced two plants, each with two seeds. How many different ways could we count this, and still get answers varying from 2 to 6?!?
More fingers, more math. One girl supported her position loudly by mentioning multiplication; two plants times two seeds would be four. Several students had made the same conclusion by different routes, but getting the kids to share their explanations that they had discussed with each other was the hard part. The confidence that they can be right is so difficult to encourage! The student who mentioned multiplication was encouraged as another student agreed with her. A 4 was written in; satisfaction all around.
So, how many seeds will he plant next? And ‘why?’
‘Four’ was the immediate answer, until a single student voice reminded us that he had to eat. So began another discussion about how to calculate the number of seeds, and how many will he eat, and how many will he have to plant? Some students felt he was going to eat two of them. (We had doubled the amount of seeds grown – we must double the amount he could eat!)
We returned to the initial instructions on page 1. A student read the evidence and told everyone definitively that only one seed would feed Jack for a whole year. By this point, I was listening to these children teaching each other how to support their facts, correct their misconceptions, and expose and correct mathematical errors. Every child was involved in this discussion – every child!
One seed eaten, three seeds planted was the ultimate conclusion. (If I rendered their discussion here, you would be as bored as we were with three years of Jack eating a seed and planting a seed!) The chart was filled in, and we were ready for the next question: if he plants three seeds, how many seeds will he have to plant the next year?
While the whole process was a conversational struggle, before I left them to this final prediction, I pointed out the table and had them write it in with their predictions. We had just begun defining a function the day before, so I asked them if they thought this was a function? I was rewarded with a student identifying the input and output terms of seeds planted and seeds grown, as x and y. Several students then made the next connection to the fact that none of the inputs we had so far would repeat, so it must be a function.
Without giving away any more of the story, I will tell you that they were able to successfully calculate the answer. We stopped here as I had them make a final prediction about the rest of the story. We will revisit Jack and his adventures in the coming unit.
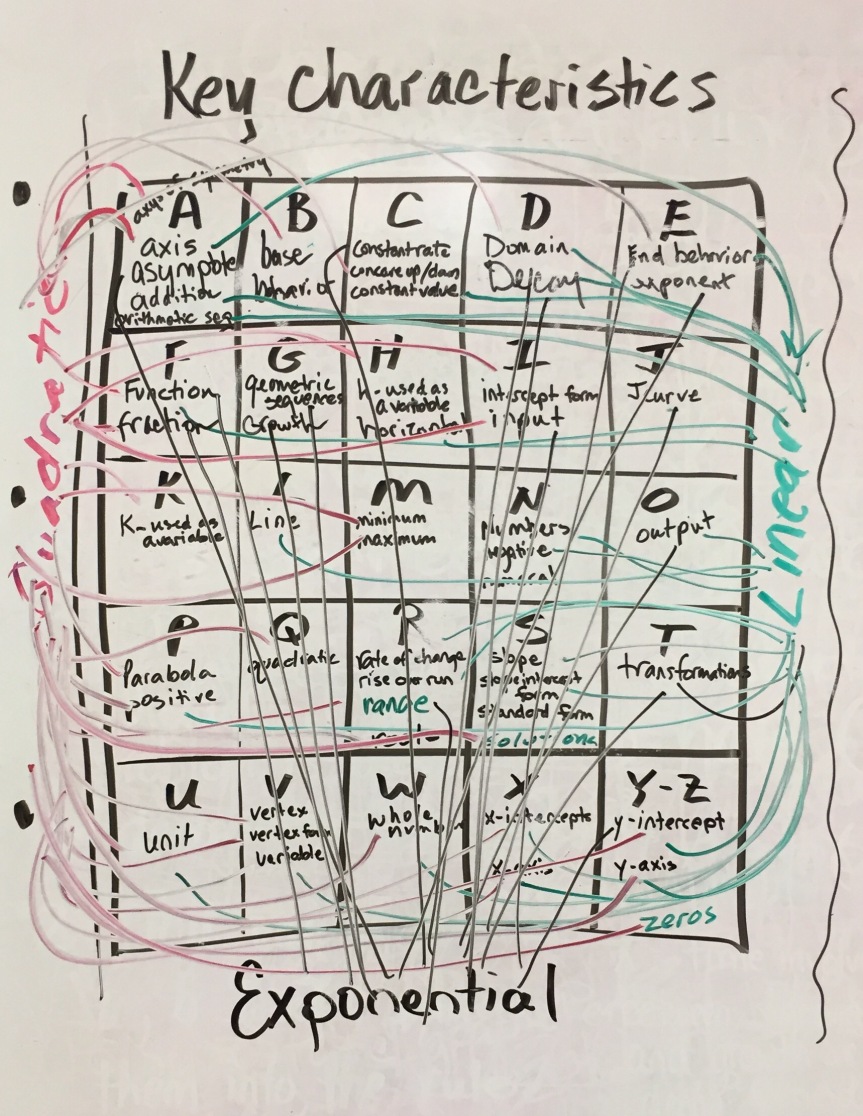
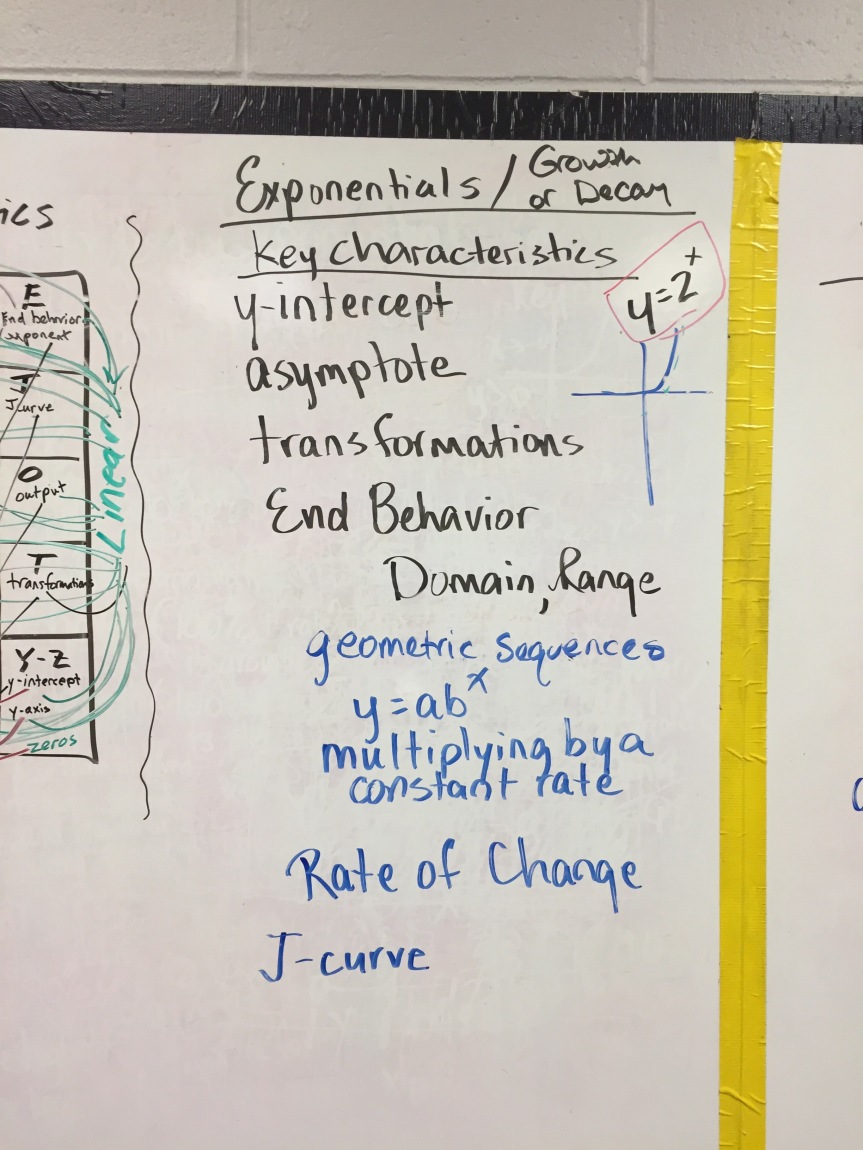
Here is the ‘after’ math:
Our school lit coach came by two days later and interviewed some of the students that had participated in the close reading. Here are some of their comments (I stayed across the room, out of their line of sight. I was curious to hear their honest responses.)
- “I liked it because it was different from the way we usually do math.”
- “Why can’t we do math like this all the time?”
- “I felt like I really understood the story.”
- “I remember more about how many fruits Jack planted.”
- “The table helped me understand.”
- “I think it will help me in my reading in other classes.”
Read that last bullet again.
‘I think it will help me in my reading in other classes.’
Wow. Now, that’s some kind of ‘after’ math!
Editor’s note: the standards for this lesson had to do with identifying functions; recognizing a function in multiple forms (such as tables), identifying functions from contextualized settings; the literary standards were identifying supporting information and using contextual clues to support mathematical arguments (a Mathematical Practice, as well). Additionally, the conversation supported mathematical reasoning, practicing vocabulary, and reasoning aloud. The constant predictions were embraced by the students, who stayed involved for what amounted to about 60 minutes of close reading. They had to know each outcome! No one read ahead, which surprised me a little. They really wanted to maintain the suspense! I can’t wait to revisit Jack and the rest of his story!
For those who notice the reading level, I wanted to use a text that would provide a low floor, and that would allow me a high ceiling – the actual math is writing and calculating an exponential equation. This was a great text for my ninth graders! The text didn’t cognitively get in the way of the activity.
To read Jack’s full story, visit Anno’s Magic Seeds, by Mitsumasa Anno. For more of her series of math books click here.